Cable and Wire

Wire, cable, strand, string, flexible rod, rope, thread and chain. So simple yet so versatile are these one-dimensional objects. They can deform by stretching, bending and twisting. They are used to transmit force, energy and signals over long distances - generate signals by their own dynamics in musical instruments or motion to macromolecules. This simple object can be turned into complex hoisting, knots and weaved meshes.

We explore computational models and algorithms for realtime simulation of wires and cables in virtual environments driven by a multiphysics engine.

Massless Cable	Deformation Modes	Applications in maritime, biology and robotics

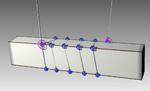
In particular, we address the challenge of combining computational speed, numerical stability and faithful physics in the presence of large mass ratios and dynamic contacts. The basic idea is that wire under high tension may be modeled as a single manybody constraint that preserve the total length of the wire, between the endpoints and an arbitrary number of sliding nodes. This is referred to as a massless cable. This model is extended to include viscoelastic properties of stretching, bending and twisting, and dry frictional contacts.

The quasistatic massless cable approach can be combined with a conventional dynamic lumped element model. An adaptive multiresolution algorithm is developed to guarantee numerical stability at high tension while allowing slacking at low tension and provide optimal tradeoff between computational speed and versatile dynamics.

Publications

C. Lacoursière, F. Nordfeldth, and M. Linde. A partitioning method for parallelization of large systems in realtime. IMSD2014-ACMD2014: The 3rd Joint International Conference on Multibody System Dynamics, The 7th Asian Conference on Multibody Dynamics, BEXCO, Busan, Korea, June 30 - July 3 (2014). abstract

M. Servin, C. Lacoursière, and K. Bodin. Hybrid, multi-resolution wires with massless frictional contacts. IEEE Transactions on Visualization and Computer Graphics, Volume: 17 Issue:7, On page(s): 970 - 982, July (2011). IEEE computer Society Digital Library. IEEE Computer Society, <http://doi.ieeecomputersociety.org/10.1109/TVCG.2010.122>, pdf

M. Servin, C. Lacoursière, and F. Nordfelth. Adaptive resolution in physics based virtual environments. SIGRAD 2008, Stockholm, Sweden, (2008). pdf, web

M. Servin and C. Lacoursière. Rigid body cable for virtual environments. IEEE Transactions on Visualization and Computer Graphics, 14:783-796 (2008). pdf, web

J. Zakrisson, K. Wiklund, M. Servin, O. Axner, C. Lacoursière, and M. Andersson. Rigid multibody simulation of a helix-like structure: the dynamics of bacterial adhesion pili. European Biophysics Journal, Vol 44 (5), pp 291-300 (2015). doi: 10.1007/s00249-015-1021-1, pdf preprint

M. Servin and C. Lacoursière. Massless cable for real-time simulation. Computer Graphics Forum, vol 26, no. 2, 172-184 (2006). pdf, web