DEM

Abstract

The smooth and nonsmooth approaches to the discrete element method (DEM) are examined from a computational perspective. The main difference can be understood as using explicit versus implicit time integration. A formula is obtained for estimating the computational effort depending on error tolerance, system geometric shape and size, and on the dynamic state. For the nonsmooth DEM, a regularized version mapping to the Hertz contact law is presented. This method has the conventional nonsmooth and smooth DEM as special cases depending on size of time step and value of regularization. The use of the projected Gauss-Seidel solver for nonsmooth DEM simulation is studied on a range of test systems. The following characteristics are found. Firstly, the smooth DEM is computationally more efﬁcient for soft materials, wide and tall systems, and with increasing ﬂow rate. Secondly, the nonsmooth DEM is more beneﬁcial for stiff materials, shallow systems, static or slow ﬂow and with increasing error tolerance. Furthermore, it is found that just as pressure saturates with depth in a granular column, due to force arching, also the required number of iterations saturates and become independent of system size. This effect make the projected Gauss-Seidel solver scale much better than previously thought.

Videos

Drum rotating with 0.13 rad/s and 7500 particles
This simulation shows a drum rotating with 0.13 rad/s, drum diameter 0.8 m and 7500 spherical particles of 0.01 m diameter size. Click here to follow our video channel which has more simulations of many configuration and played with different speeds.

Drum rotating with 0.63 rad/s and 7500 particles
This simulation shows a drum rotating with 0.63 rad/s, drum diameter 0.8 m and 7500 spherical particles of 0.01 m diameter size. Click here to follow our video channel which has more simulations of many configuration and played with different speeds.

Drum rotating with 2.51 rad/s and 7500 particles
This simulation shows a drum rotating with 2.5 rad/s, drum diameter 0.8 m and 7500 spherical particles of 0.01 m diameter size. Click here to follow our video channel which has more simulations of many configuration and played with different speeds.

Calculator

Formula:

\begin{equation*} \begin{array}[l] \\ \frac{\tau_{{\tiny NDEM}}}{\tau_{{\tiny SDEM}}} = \sqrt{\frac{ \max\left(\epsilon^2 m v{n}^2, 2\epsilon mgd\right)}{kd^2}} \frac{K^{{\tiny GS}}_{{\tiny NDEM}}}{K{{\tiny SDEM}}} \frac{N_{c}}{N_\text{p}}\cdot\nonumber\\ \quad\quad\quad\cdot\frac{c_0 (1 + c_1 I )}{\epsilon} \left\{ \begin{array} [l]{lr}% w( 1 - \exp[-\tfrac{c_2 l} {w}]) & \text{ , if } w \gtrsim 5\\ c_2 l & \text{ , if } w < 5 \end{array} \right.\\ \frac{}{}\\ \frac{}{}\\ \tau_{\tiny SDEM} = \sqrt{\frac{k}{m}} K_{\tiny SDEM}N_{\text{p}}\tau_{\text{real}}\\ \frac{}{}\\ \frac{}{}\\ \tau_{\tiny NDEM} = \frac{K^{\tiny GS}_{\tiny NDEM}N_{\text{it}} N_{c}} {\min\left(\epsilon\frac{ d}{v_{n}}, \sqrt{\frac{ 2\epsilon d}{g}}\right)}\tau_{real}\\ N_{\text{it}}^{\epsilon} (l,w,I) = \tfrac{c_0 (1 + c_1 I )}{ \epsilon } \left\{ \begin{array} [l]{lr}% w( 1 - \exp[-\tfrac{c_2 l} {w}]) & \text{ , if }w \gtrsim 5\\ c_2 l & \text{ , if }w < 5 \end{array} \right. \end{array} \end{equation*}

System configuration:

$g$ :		[${\tiny m/s^{2}}$]	$\rho$ :		[${\tiny kg/m^3}$]	$\nu$ :
$K_{\tiny SDEM}$ :				$K^{\tiny GS}_{\tiny NDEM}$ :
$c_0$ :	0.3		$c_1$ :	2.0		$c_2$ :	0.44

Evaluate the time here:

$\epsilon$ :			$w$ :			$l$ :
$I$ :			$Y$ :		[GPa]	$d$ :		[m]

$\frac{\tau_{{\tiny NDEM}}}{\tau_{{\tiny SDEM}}}$ :		$\frac{\tau_{{\tiny SDEM}}}{\tau_\text{real}}$ :		$\frac{\tau_{{\tiny NDEM}}}{\tau_\text{real}}$ :
$h_{N}$ :	[ms]	$h_{S}$ :	[ms]
$N_\text{P}$ :		$N_\text{it}$ :		$V_{n}$ :	[m/s]

Input all values. Selected value (red colored) will be used as domain variable.

$I$:

0~

$w$:

[d]

$l$:

[d]

Input all values. Selected value (red colored) can have multi (< 8) values, each correspond to one curve

$\epsilon$:

Input 1~ values

$Y$:

[Pa]	[Pa] Input 1~ values

$d$:

[m]	[m] Input 1~ values

Related plots

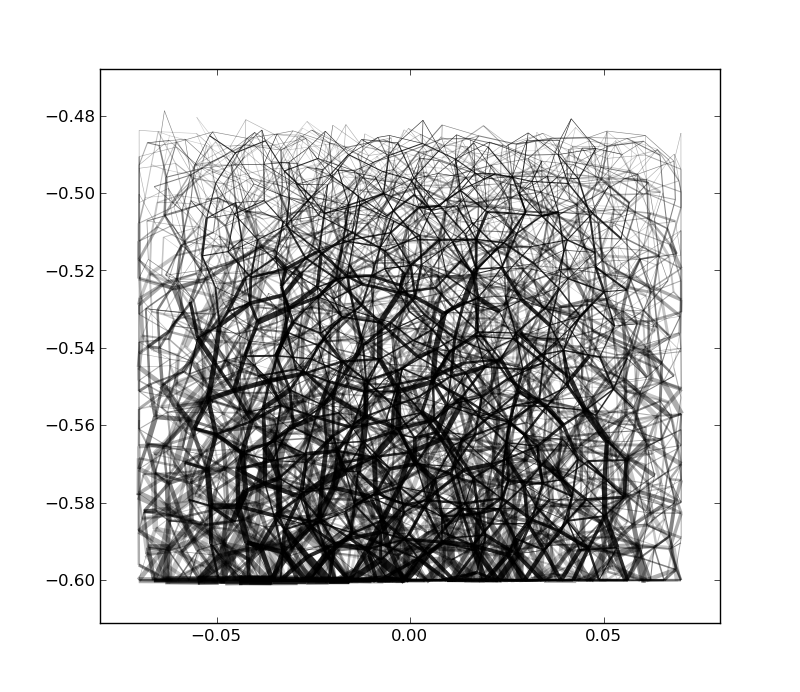
Force network
The contact forces form force networks. These are weighted graphs with the particles as nodes and contact forces as edges. We use the normal force magnitude for the edge weight. In granular materials with too few iterations the strong force chains that are a characteristic feature of granular materials do not appear. Instead, the force distributes as the hydrostatic pressure in a fluid, i.e., increases linearly with depth from the top surface. When increasing the number of iterations, strong force chain structures emerge and with this the pressure force saturate and become independent of depth in the column. This is the well-known Janssen effect of granular materials, which is due to an arching effect of the force chains whereby the container walls carry part of the weight of the material Click here for more force network figures.

Velocity fields
On sufficiently large scales of length and time a granular material may be considered as a continuous solid represented by continuous fields of mass distribution, flow velocity and stresses and strains. The averaging process of sampling microscopic particle properties and inter-particle forces to macroscopic quantities is referred to as coarse graining (or homogenization). A cubic grid is introduced and the fields are evaluated at the grid points. The smoothing length is chosen to 1.5 times particle diameter and we use grid size L = 0.5 d. Click here for more velocity fields

Scalar fields
On sufficiently large scales of length and time a granular material may be considered as a continuous solid represented by continuous fields of mass distribution, flow velocity and stresses and strains. The averaging process of sampling microscopic particle properties and inter-particle forces to macroscopic quantities is referred to as coarse graining (or homogenization). A cubic grid is introduced and the fields are evaluated at the grid points. The smoothing length is chosen to 1.5 times particle diameter and we use grid size L = 0.5 d. Click here for more scalar field plots of mass density, pressure, strain rate and inertial number.

Pseudo code